130
Zhang
et al
.,
Improved online sequential extreme learning machine for simulation of daily reference evapotranspiration
Tecnología y Ciencias del Agua
, vol. VIII, núm. 2, marzo-abril de 2017, pp. 127-140
•
ISSN 2007-2422
Hargreaves, Mc-Cloud, and Priestley-Taylor
models. First, the
ET
0 values of four cities were
calculated using the FAO-56 PM. Then, the stan-
dard formula evapotranspiration calculation for
all empirical models is shown.
(1) FAO-56 Penman-Monteith:
ET
0
=
0.418
R
s
G
(
)
+
900
T
+
273
u
2
e
s
e
a
(
)
+
1
+
0.34
u
2
(
)
(1)
The original meteorological data of
T
max
,
T
,
T
min
,
n
,
Uh
,
RH
m
,
φ
and
Z
were used in the
model:
(2) Hargreaves:
ET
0
=
0.0023
R
a
T
+
17.8
(
)
T
max
T
min
(
)
1
2
(2)
T
max
,
T
,
T
min
,
n
and
φ
were used in the model:
(3) Mc-Cloud:
ET
0
=
0.254 1.07
(1.8
T
)
(3)
Only
T
was referred to in the model:
(4) Priestley-Taylor
ET
0
=
1.26
+
R
n
G
(
)
(4)
T
max
,
T
,
T
min
,
n
and
φ
were used.
However, these variables are obtained
directly or indirectly from the meteorological
raw data (
Uh
,
T
,
RH
,
T
min,
T
max,
n
,
φ
and
Z
).
Furthermore, the calculation formula for them
did not have a precise formula by estimation or
experience.
Therefore, the inputs
Uh
,
T
,
RH
,
T
min,
T
max,
n
,
φ
and
Z
, the
ET
0 output were calculated
by the FAO-56 PM method and used for the
calibration of the IOS-ELM models. The mean
absolute error (MAE), the root mean square
error (RMSE), effectiveness index of the model
(EF) and self-correlation coefficient (
R
2
) statistics
were used for the assessment criteria of the
models in this study. EF model efficiency mainly
depends on the Nash coefficient EF values; as
the values approach one, the efficiency of the
model increases. The study adopted the calcula-
tion model of the validity index for EF by Nash
and Sutcliffe.
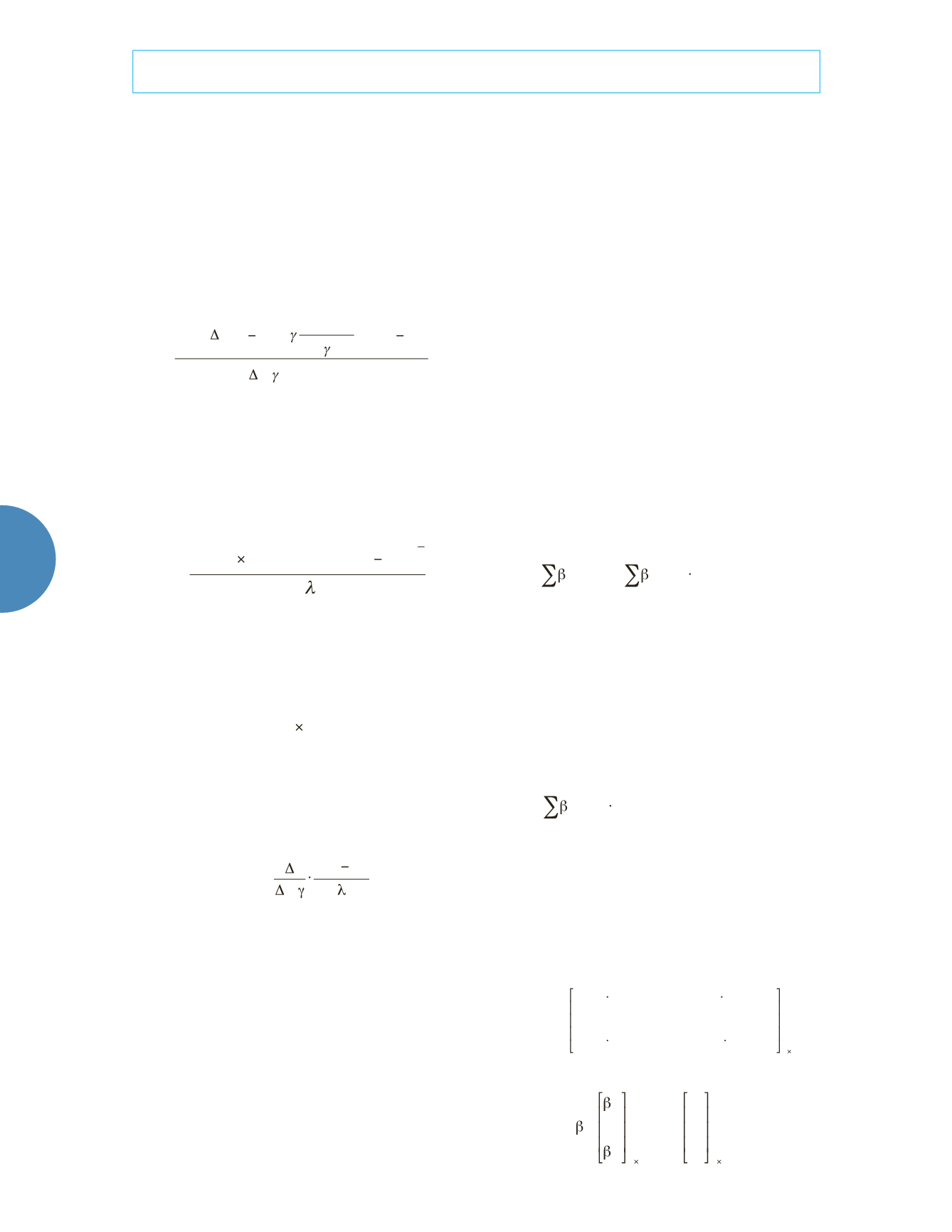
Extreme learning machine (ELM)
For
N
random distinct samples (
x
i
,
t
i
) where
x
i
= [
x
i
1
,
x
i
2
,...,
x
in
]
T
∈
R
n
,
t
i
= [
t
i
1
,
t
i
2
,...,
t
in
]
T
∈
R
m
and
for the standard SLFNs (
Ñ
hidden nodes), the
activation function
g
(
x
) is expressed as:
i
i
=
1
Ñ
g
i
x
i
( )
=
i
i
=
1
Ñ
g w
i
x
j
+
b
i
(
)
=
0
j
j
=
1,...,
N
(5)
where
w
i
= [
w
i
1
,
w
i
2
,...,
w
in
]
T
is the weight vector
connecting the ith hidden node and the input
nodes,
b
i
= [
b
i
1
,
b
i
2
,...,
b
in
]
T
is the weight vector
connecting the ith hidden node and the output
nodes and
b
i
is the threshold of the ith hidden
node.
i
i
=
1
Ñ
g w
i
x
j
+
b
i
(
)
=
t
j
j
=
1,...,
N
(6)
The above N equations can be written com-
pactly as
H
b =
T
(7)
where
H w
,
b
,
x
(
)
=
g w
1
x
1
+
b
1
(
)
L
g w
Ñ
x
1
+
b
Ñ
(
)
M L
M
g w
1
x
N
+
b
1
(
)
L
g w
Ñ
x
N
+
b
Ñ
(
)
N Ñ
(8)
=
1
T
M
Ñ
T
Ñ m
,
T
=
t
1
T
M
t
N
T
N m
(9)


