35
Tecnología y Ciencias del Agua
, vol. VIII, núm. 2, marzo-abril de 2017, pp. 31-41
Li
et al
.,
Particle size distribution and settling velocity of sediments in water diverted from the Yellow River during border-strip irrigation
ISSN 2007-2422
•
formula used to calculate the probability of
incipient motion of sediments are commonly
used and can produce satisfactory results. The
calculation and analysis performed in this study
suggest that introducing a shape factor into
Wu’s formula can yield a universal formula for
determining settling velocity, but the method
proposed by Fan, Zhong and Wu (2012) is more
applicable to the case of sediment in irrigation
water diverted from the Yellow River. In this
study, a settling velocity calculation was per-
formed to verify Fan’s method. A comparison of
the calculation results with the measured data
suggests that water flow over the strips can be
simplified to open-channel flow. The relation-
ship of the settling velocity of particles to the
Shields number and other parameters can be
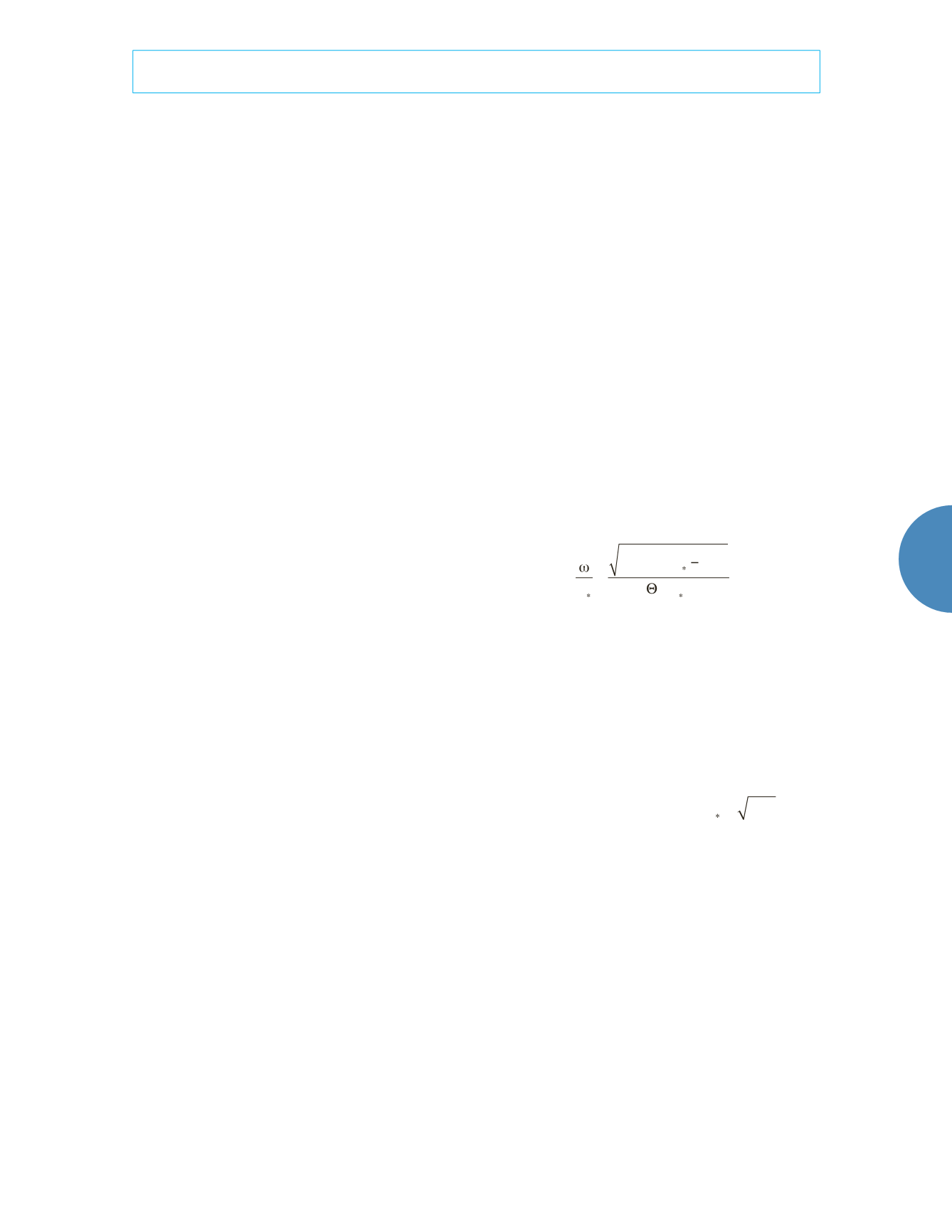
expressed as follows:
u
=
25
+
1.2
d
2
5
(
)
1.5
0.5
d
1.5
(1)
where the Shields number is given by
Q
=
D
hJ
/
D
,
in which
h
is water depth,
d
*
= (
D
g
/
v
2
)
1/3
D
,
J
is
the slope of water surface, and
D
represents
dimensionless particle size. In
D
= (
r
s
–
r)/r
,
r
s
is the sediment density,
r
is the fluid density,
g
is gravitational acceleration, and
v
is the fluid’s
kinematic viscosity.
The friction velocity of a fluid is normally
calculated using the equation,
U
=
gHj
where
J
denotes the hydraulic slope,
H
is water depth,
and
g
is gravitational acceleration (Liu, Li, &
Wang, 2005).
Results and analyses
Analysis of advance rate of irrigation water
As figure 3 shows, the advance rate of water
flow over the field gradually decreased along
the strip length. The advance rate over the first
80 m of the narrow strip was significantly higher
than the rate over the same section of the wide
strip. The water underwent a rapid increase in
advance rate as it flowed over the section of the
three times, compared with oven dry method
for soil water content, during the experimen-
tal period. Every steps as follow: insert the
TDR probe and the soil auger into soil and
let them stay parallel, meanwhile measure
the TDR and the soil moisture content. And
choose three different time periods when the
soil moisture content is different, such as 2
days before irrigation, 2 days after irrigation,
15 days after irrigation. The relation curve
was obtained between soil moisture content
and soil depth calibration.
3. The advance rate and settling speed of sedi-
ment in the irrigation water were measured
during and after irrigation. The specific
procedures are as follows:
a) Before irrigation, pieces of double-layered
gauze (10 × 20 cm) were positioned on
the surface of the strips at intervals of 40
m along their length. After irrigation, the
sediment accumulated on the gauze was
weighed and then taken to the laboratory
for particle size analysis.
b) During irrigation, water samples were
collected at the outlets of the water pipes
and from locations 0 m, 40 m, 120 m, 200
m, and 280 m from the top end of each
strip. Then the concentration and particle
size distribution of the sediment in the
water samples were analyzed.
c) Two days after irrigation, undisturbed
soil samples were collected from the
strips at intervals of 40 m along their
length, and their dry bulk densities were
measured.
Calculation methods
In existing research, settling velocities of
sediment particles are typically calculated us-
ing empirical formulas, and various calculation
methods are available. Existing comparative
studies (Fan
et al
., 2012; Li, He, Zhu, & Huang,
2014) point out that the formula obtained by
Weiming Wu (Wu & Wang, 2006) through an
intensive regression analysis of the settling
velocity of irregular particles, as well as the


