154
Wei
et al
.,
Water table response to a pumping test in the hinterland core area of the Taklimakan Desert, China
Tecnología y Ciencias del Agua
, vol. VIII, núm. 2, marzo-abril de 2017, pp. 151-158
•
ISSN 2007-2422
barometric pressure on the water level cannot
be ignored compared to the larger circum-
stances (such as the late period pumping test),
it is important to perform barometric pressure
calculations in order to obtain accurate aqui-
fer parameters (Wang
et al
., 2012). During an
extended period of pumping test processes,
the delayed response, due to the transmis-
sion of the barometric pressure perturbation
through the unsaturated zone and borehole
storage or skin effects, causes a water level
difference between the aquifer and the pump-
ing well. Rasmussen and Crawford proposed
the regression deconvolution method could
be used to correct the groundwater level in
order to eliminate the influence of barometric
pressure (Rasmussen & Crawford, 1997). Af-
ter the response function
δ
(
i
)
to a barometric
pressure pulse is obtained by using ordinary
least square method linear regression, the step
response
α
(
j
)
can be found by summing the
impulse responses:
(
j
)
=
(
i
)
i
=
0
j
(1)
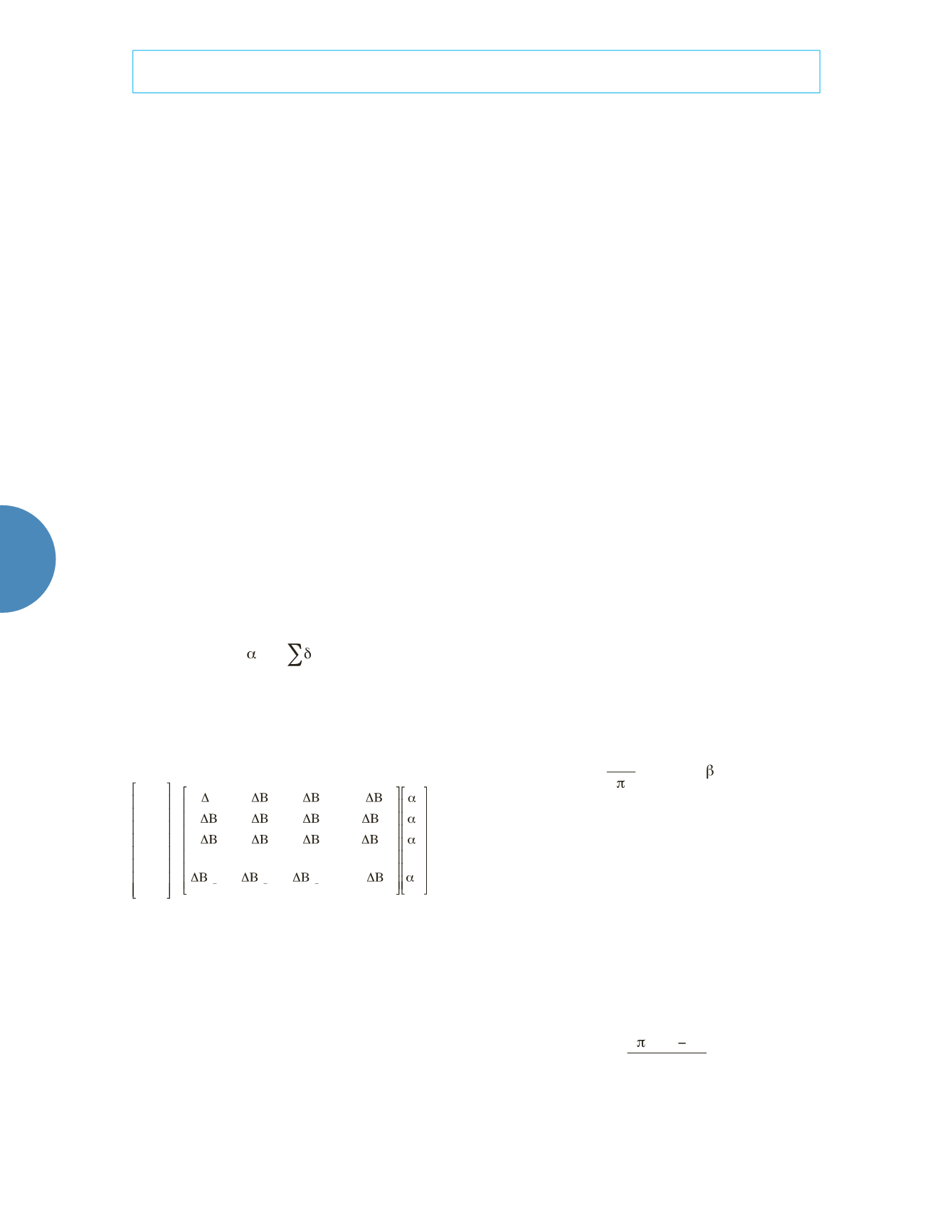
Then, it was following correction variables
of the water levels that being found (Toll &
Rasmussen, 2005):
W
m
*
W
m
+
1
*
W
m
+
2
*
...
W
n
*
=
B
1
2
3
...
m
2
3
4
...
m
+
1
3
4
5
...
m
+
2
...
...
...
...
...
n m
+
1
n m
+
2
n m
+
3
...
n
1
2
2
...
m
(2)
where
W
*
is the corrected variable for each
observation within time
t
from
m
to
n
;
Δ
B
t
is
the change in the barometric pressure at time
t
;
m
is the maximum lag selected by the user,
and
n
is the total number of observations in
the dataset.
To gain more accurate data of the water
level, we corrected the observed pumping test
data by BETCO, which is the application of the
regression deconvolution (Toll
et al
., 2005).
Calculation of hydrogeological parameters
In Aquifer Test, methods for unconfined aquifer
analysis usually are either Neuman or Boulton.
Theis with Jacob correction can also be used for
late-time of the pumping test. Due to unsteady
flow within the pumping tests by the artificial
control of water stability, we need to determine
the water level changes with time in order to
obtain hydrogeological parameters in an un-
confined aquifer of unstable movement. In this
paper, the Neuman model, the Boulton model,
and the Theis model with the Jacob correction
(Theis with Jacob) for unconfined aquifer are
used to fit the water level variation curve of the
pumping process.
Jacob (1940) proposed the following
correction:
s
cor
=
s
– (
s
2
/2
D
)
(3)
Where
s
cor
is the corrected drawdown,
s
is the
measured drawdown, and
D
is the original satu-
rated aquifer thickness. There are no additional
type curve parameters for this solution method.
The equation developed by Neuman repre-
senting drawdown in an unconfined aquifer is
given by (Neuman, 1975):
s
=
Q
4
T W u
A
,
u
B
,
(
)
(4)
Where
W
(
μ
A
.
μ
B
.
β
)
is known as the uncon-
fined well function;
μ
A
= r
2
s/
4
Tt
is the Type A
curve for early time steps;
μ
B
= r
2
S
y
/4
Tt
is the
Type B curve for later time steps;
β
= r
2
K
v
/K
H
,
K
V
,
K
H
: vertical and/or horizontal permeability;
r
is the distance to the observation well;
S
is stor-
ativity;
S
y
is
specific
yield, usable probe volume;
T
is transmissivity.
The method developed by Boulton (1963)
can be performed as follows:
s
D
=
2
T
(
H D
)
Q
(5)
Where
H
is defined as the average head along
the saturated thickness, and other parameters
defined as mentioned above.


