58
A
vances
en
la
hidráulica
de
redes
de
distribución
de
agua
potable
La solución numérica requiere de condiciones iniciales y de frontera. Las condiciones ini-
ciales en este caso están dadas por los valores de la concentración en todos los puntos de la
tubería para el momento
t=0
que se suponen conocidos o se determinan para una solución
de estado permanente. La condición de frontera se aplica a la frontera izquierda y consiste
en tener los valores de la concentración para
x=0
durante el período de tiempo que se va a
considerar. Si la tubería parte de una fuente éstos serán los valores de la concentración en
la fuente. Si la tubería parte de la unión de varias tuberías, las concentraciones para
x=0
se
calculan por las contribuciones de las tuberías que confluyen en la unión, como se explica
más adelante en el algoritmo de solución para una red.
La solución avanza en el tiempo en incrementos consecutivos
Δt
ca
. En cada incremento se
calcula la concentración en todos los puntos de la tubería por el esquema mostrado en la Fi-
gura 1.2.4. Este esquema proviene del método de las características y de la solución analítica
de la ecuación (1.2.10).
Cuando la división de subtramos cambia de un período hidráulico a otro, se aplica una
interpolación para obtener los valores de concentración en los puntos de la nueva división;
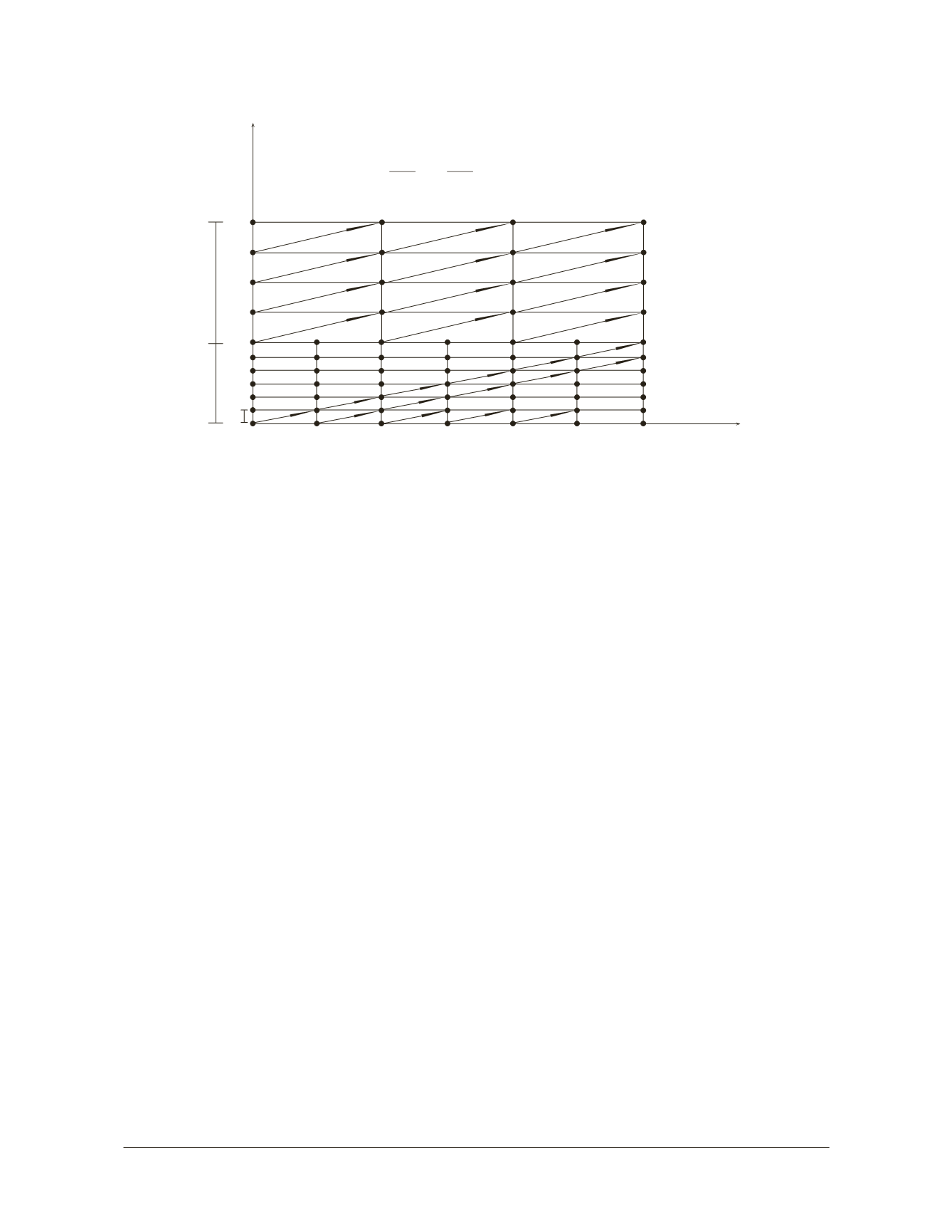
ver Figura 1.2.3.
1.2.5 S
olución
para
una
red
Se asume una
mezcla completa
del agua en los nodos de la red. El concepto de mezcla com-
pleta en un nodo de la red asume que el agua que ingresa con diferente concentración por
parte de las tuberías que confluyen en el nodo, se mezcla en éste obteniéndose una nueva
concentración que será igual para todas las tuberías cuyos caudales salen del nodo. La con-
dición de continuidad de masa en el nodo se expresa entonces como
Figura 1.2.3 Solución numérica de la ecuación de convección.
t
PROCEDIMIENTO DE SOLUCIÓN NUMÉRIC DE LA ECUACIÓN DIFERENCIAL DE ADVECCIÓN
t
h
x
l = 0
x x = L
t
CA
t
C V X
C KC
0
2
2
2
2
+ - =
D
D
D
t
h


