72
A
vances
en
la
hidráulica
de
redes
de
distribución
de
agua
potable
Para dar solución a estos dos problemas Aldama
et al
. (1998) proponen un nuevo método
general para la consideración de las condiciones de frontera y para una solución numérica
eficiente de problemas de ecuaciones diferenciales en redes, llamado
método de las funciones
de Green numéricas
. Este método se aplica en el presente trabajo para obtener una solución
numérica eficiente. Las bases del método se explican en Aldama
et al
. (1998); por esta razón
aquí se explica solamente el procedimiento computacional correspondiente al presente mo-
delo de transporte en redes.
Para la solución numérica se utiliza la misma discretización que se usa en la etapa lagrangia-
na. Las derivadas se aproximan por diferencias finitas como sigue:
t
C C C
,
t
j n
j
a
1
a
2
2
.
D
-
+
1. 3.18
+
+
- +
+
-
1
1
+ +
c
x
C
x
C
C C
x
C C C
2
1
2
2
1
,
,
,
j
n 1
j n 1
j
n 1
j
a
j
a
j
a
2
2
2
2
1
2
2
.
D
D
+
- + -
m
1. 3.19
donde el superíndice
a
señala valores obtenidos en la etapa lagrangiana. Las ecuaciones (3.18)
y (3.19) se sustituyen en (3.11), obteniéndose en resultado las siguientes ecuaciones para los
puntos interiores (sin incluir los dos extremos) de una tubería:
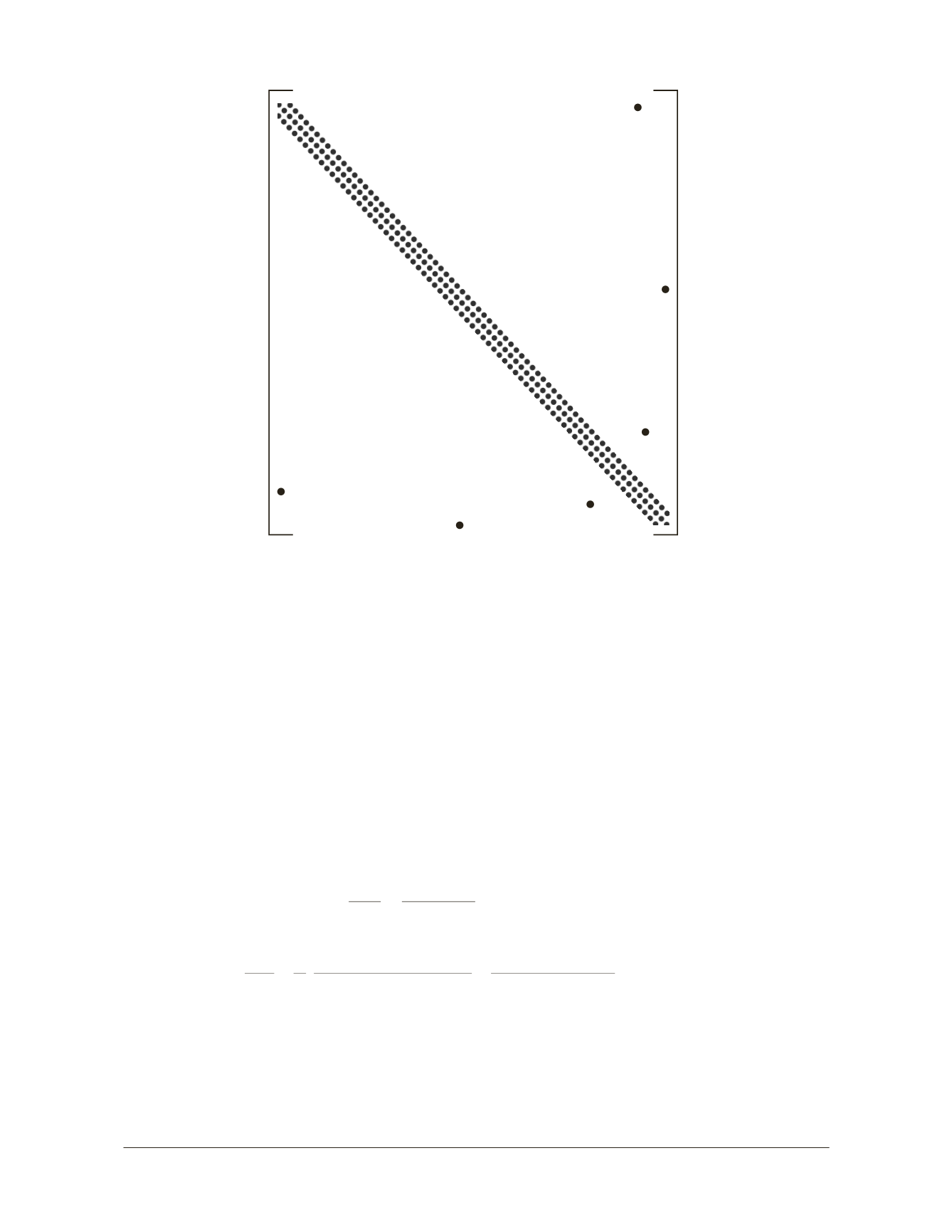
Figura 1.3.5 Estructura de la matriz resultante para la red de la Figura 1.3.4


