Anexo
128
Expresado en forma sencilla, el modelo clásico supone que el término de perturbación relacionado
con una observación cualquiera no está influido por el término de perturbación relacionado con
cualquier otra observación.
Se tomaron en cuenta 3 distintas pruebas para demostrar no autocorrelación en el modelo; el
estadístico Durbin-Watson, la prueba del correlograma y la de LM test.
1) Durbin-Watson:
además de la observación directa del gráfico de residuos, el estadístico
Durbin-Watson, es la forma más habitual de contrastar la existencia de autocorrelación de
primer orden. A partir de este estadístico se puede interpretar que:
• Si hay autocorrelación positiva las diferencias entre residuos que distan un
periodo es muy pequeña por lo que el valor del estadístico será próximo a
cero.
• Si hay autocorrelación negativa los residuos serán prácticamente iguales
pero de signo contrario, su diferencia será por tanto grande y el estadístico
será más próximo al límite superior que se establece en cuatro.
• Si no hay autocorrelación, la relación entre los residuos será intermedia y
por tanto, el valor del estadístico experimental también alcanzará un valor
intermedio.
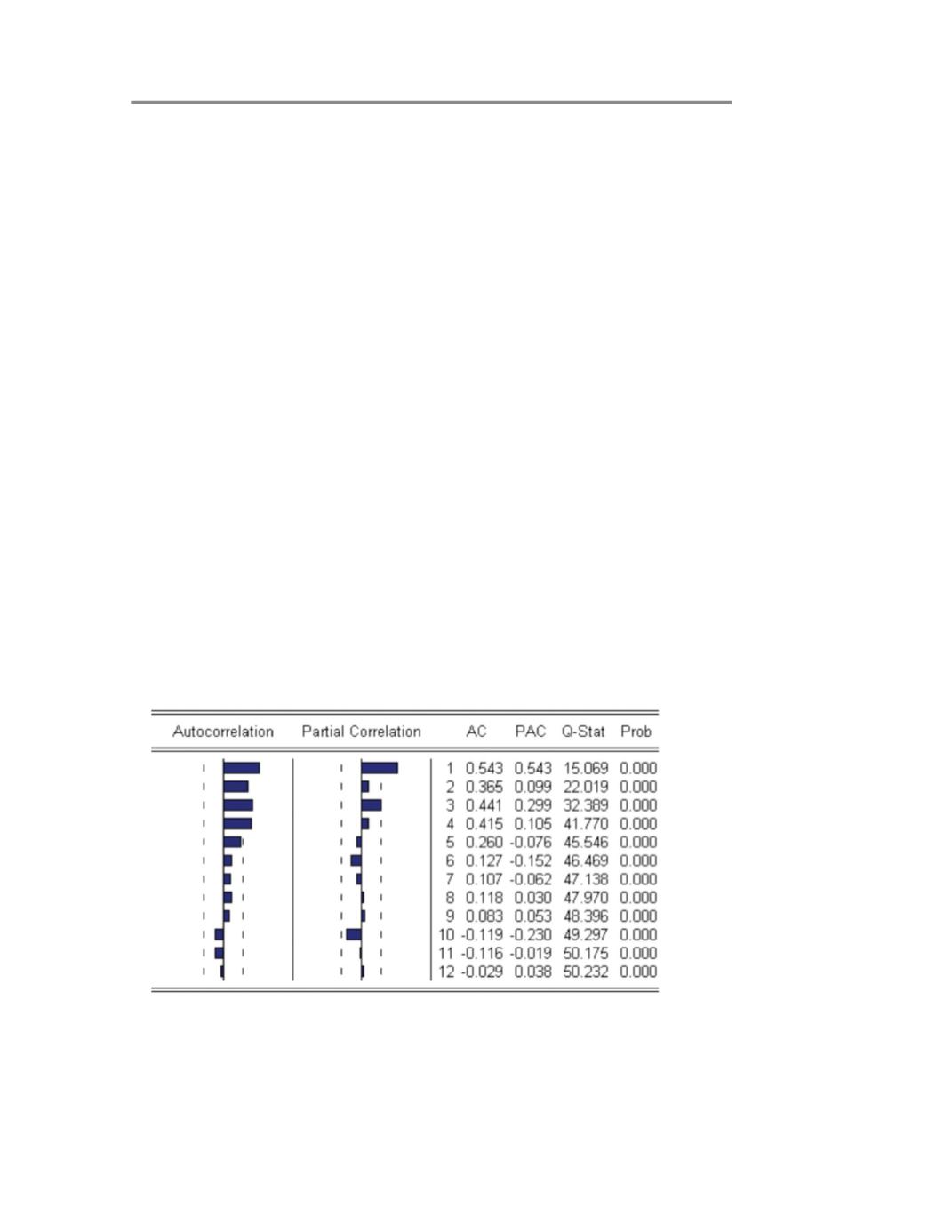
2) Prueba del correlograma:
la autocorrelación, está representada gráficamente (Figura A2)
en la primera y numéricamente en la tercer columna con el nombre de AC, su línea vertical
continua representa el cero y las punteadas sus límites de confianza; las barras a su izquierda
expresan valores negativos y las de la derecha positivos. Si ninguna autocorrelación rebasa
los límites de confianza, se acepta la hipótesis nula considerando que los coeficientes de
autocorrelación no son significativamente diferentes de cero.
Figura A. 2 Correlograma de residuos


